The diffraction grating

If we have loaded a crystalline specimen into the electron microscope and we press the ‘diffraction’ button, then what we see is grid of bright spots. People often say this grid (which is usually incomplete – only a few bright spots are lit up, unless the specimen has been accurately aligned) is ‘like a diffraction grating pattern’. It is like a diffraction grating pattern, although in fact, unlike the pattern we would obtain from an optical diffraction grating, the behaviour of an electron diffraction pattern is made more complicated by the thickness of the object and multiple (dynamical) scattering.

I still think it is worth rehearsing the behaviour of a conventional (optical) diffraction grating before we try to discuss three-dimensional electron diffraction effects. There three reasons for this: 1) diffraction from periodic (crystalline) arrays of atoms is absolutely key in electron imaging, and so we may as well spend some time understanding fully the simplest example of diffraction from a one-dimensional periodic object; 2) the diffraction grating can give us a qualitative insight into the nature of the convolution theorem; 3) the diffraction grating can illuminate, in a physical way, the difference between the Fourier integral and the discrete Fourier transform.

Lets just recall how we constructed our sinc function. We took the Fourier transform of a top hat function which looked like this

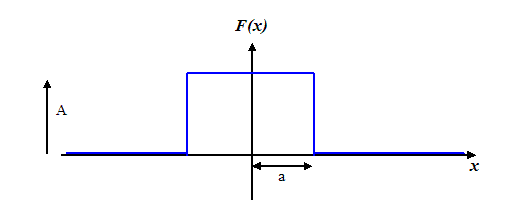
in order to find the amplitude of the Fraunhofer diffraction pattern. Now lets think about taking the Fourier transform (that is, forming the Fraunhofer diffraction pattern) of not a continuous top-hat function, but one made up of a series of spikes, like a hair comb. Physically, we would construct this from a series of equally-spaced slits – a diffraction grating. The functional form of the exit wave emerging immediately behind the grating looks like this:

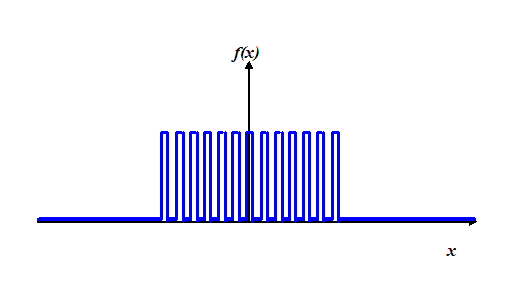
To begin with, let’s assume each spike in this function is infinitesimally narrow. We can use our mechanical Fourier transform machine to calculate what the diffracted amplitude will look like a very long way from the grating, as a function of angle. I want to think about this by considering more and more slits, starting off with just two slits. In other words, a series of functions that looks like this:

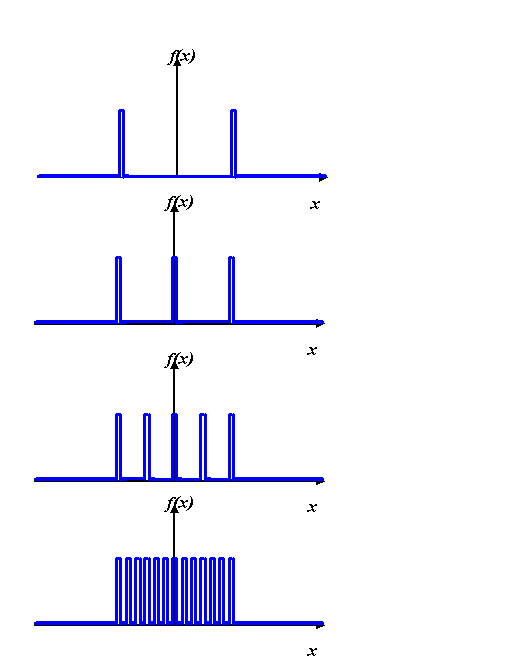
In the complex plane, we will have wave value vectors for these four examples that, at some small scattering angle, add like this:

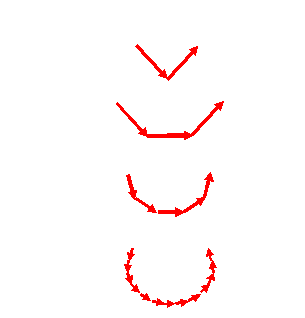
At we increase the scattering angle, the vectors rotate, changing the resultant vector, which, as before, we draw between the two ends of chain of wave vectors. Of course, in the limit of infinitely many tiny slits, we tend towards the chain being a continuous line, like in our calculation of the sinc function. At the opposite limit of just two slits, we just have our Young’s slits amplitude distribution. It doesn’t take much imagination to think through what will happen to the resultant vectors, as a function of scattering angle, between these two extremes. Qualitatively, for an increasing number of slits, the diffracted amplitude looks like this:

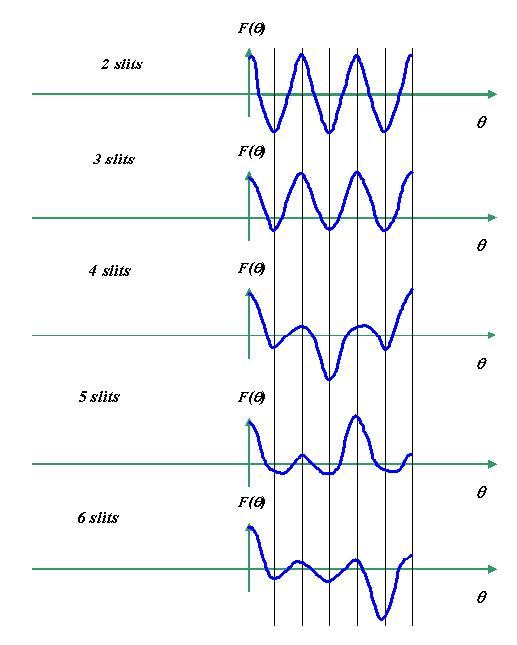
These diagrams are not quantitatively accurate (I did them using the mouse and the curve ‘autoshape’, so they are a bit wonky – the crossing points and magnitudes are purely qualitative). What’s happening is that as we increase the number of slits, then the ‘snake’ of added component vectors writhes around in a tighter and tighter bundle. Every so often, the bundle straightens out into a large magnitude. For two slits, the first maximum magnitude occurs on the first vertical line (above), and is purely negative. For three slits, it occurs on the second line, and is positive. For four slits, the first maximum magnitude occurs on the third line, and is negative, and so on and so forth.

Aside: We might infer from these diagrams that the complex value of a diffraction pattern from an array of atoms changes very dramatically depending on whether we have an even or an odd number of atoms across the width of a crystallite. Well, that's not quite true. The way we've constructed our distribution of slits (atoms) here means that an even number of slits appear shifted (by half their spacing) along the x-axis relative to the case of an odd number of slits. This shift is really responsible for the positive and negative peaks in the amplitude, because a shift introduces a phase ramp across the Fourier transform. Because here we have arranged to keep the result purely real (by keeping the slits symmetric about the origin), then this phase change results in a π shift in some of the even-slit diffraction peaks. Don't worry about it... :end of aside

The pattern repeats itself at equal intervals. I haven’t drawn negative values of θ: all these graphs are symmetric about the origin. As the number of slits is increased, the big peaks migrate to larger values of θ, until eventually we are just left with a single peak at the origin in the shape of a sinc function. At this stage, our comb of infinitesimally tiny gaps has blurred into just a top hat function. Physically, we are adding up an infinite number of secondary waves, according to Huygen’s Principle.

Most textbooks derive the intensity distribution of these peaks, which of course will miss out the subtleties of the change of sign of the amplitude. The intensities, which is of course is what we see when we do a diffraction experiment, look (very roughly) like this:

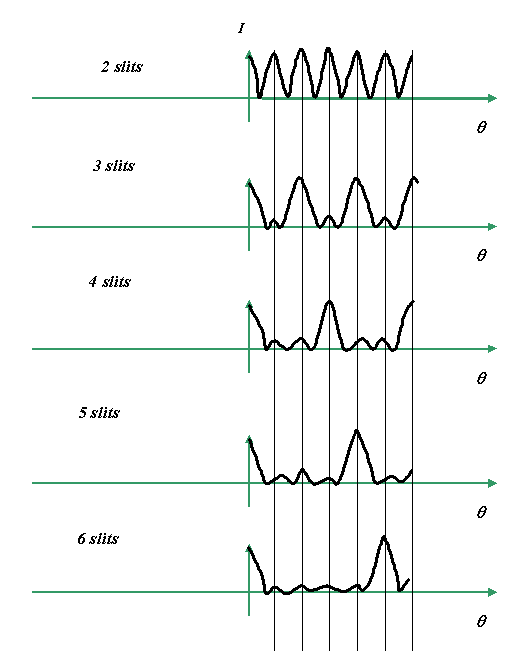
Looking the intensity, the pattern of the evolution of the grating pattern becomes a little bit clearer. The first peak from an N-slit grating occurs at δθ(N-1), where δθ is the angle of the first maximum in a Young’s slits experiment, where the separation of the slits is the width of the grating. This is usually taught as occurring when there is an integral number of wavelengths in the path difference between adjacent slits. Obviously, when this occurs, all the little contributing wave vectors come back into phase with another, and so the ‘writhing snake’, which produces all the subsidiary peaks between the main diffraction maxima, suddenly straightens out.

We can think of this another way. Instead of having a fixed width of the whole grating, and then adding more and more slits each spaced by a smaller distance, we could think of adding more and more slits each separated by the same distance. In this case, the scattering angle of the diffraction peaks remains constant, but the width of the peaks decrease as N, the number of slits, is increased. This is much more like scattering from a periodic array of atoms. The total width of a given crystallite determines the clarity (or sharpness) of a diffraction peak (indeed, this fact can be used to estimate crystallite size in both X-ray and electron diffraction, via the Scherrer formula). In optical spectroscopy, the chromatic resolution of a diffraction grating is proportional to the number of slits for the same reason. In fact, in any practical set up (optical, X-ray or electron) the actual width of diffraction peaks is often determined by the angular size of the illuminating wave field: in other words, its spatial coherence.

Copyright J M Rodenburg