The electron as a wave:
We can imagine a free electron wave travelling along a one-dimensional line (a ray or beam) as a corkscrew, of the sort you might use to open a bottle of wine.
Experiment: Take a corkscrew and let a light cast its shadow onto a flat surface. The shadow looks like this:
Now when introducing the electron wave, many textbooks and informal discussions start by drawing a picture of the shadow of a corkscrew (as shown above), and they then describe this shadow as being 'like an electron wave'. In fact, this wavy-line model of the electron wave is a central cause of great confusion amongst non-physicists. If in doubt, never think of an electron wave as being a wave-like shadow of a corkscrew: think of the corkscrew itself.
Hold the corkscrew horizontally and examine it in detail. It is a continuous spiral. The radius of the corkscrew is constant at all points along its length. At any particular point along its length, the edge of the corkscrew describes a certain angle with repect to the horizontal, which is shown in blue in the diagram below. This angle is called the phase of the electron wave. Still holding the corkscrew horizontally, look along the axis of spiral. If we marked off any particular position along the length of the corkscrew, we could draw a line between the centre of the corkscrew and the position of its edge at that exact position. The picture would look like this:
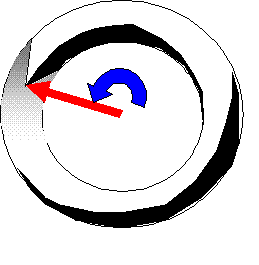
We draw the red line as a vector, which just means a pointer extending from the centre of the corkscrew to its edge. This vector, which is called the value of the wavefunction, has two numbers associated with it. Any particular vector, which can point in any direction and have any length, can always be made up of two vectors, like this:
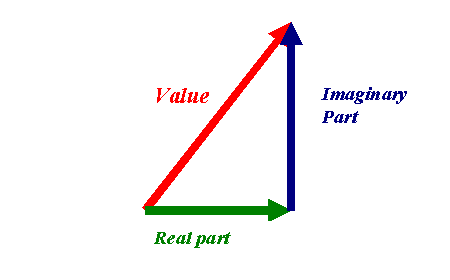
The horizontal vector is called the real part of the value of the electron wavefunction, the vertical vector is called the imaginary part of the value of the electron wavefunction. It is essential to remember that any travelling electron wave - that is, a wavefunction that represents an electron which is moving through space, is made up of real and imaginary parts: it is a complex function.
If you are unfamiliar with complex numbers, just remember the corkscrew. The corkscrew exists in three-dimensional space, but it represents just a one-dimensional wave function that exists along a single line. The crucial thing to remember is that we need two numbers to describe the edge of the corkscrew at any particular point along the line.
Some non-physicists find this complex number thing quite terrifying. Indeed, the words 'complex' and 'imaginary' imply untold mysteries and unfathomable difficulties. Do not fear - if you understand how a corkscrew works, you understand almost everything you need to know about complex numbers, at least in the context of electron microscopy.
Mathematical notation
Although this introduction is as un-mathematical as possible (for material scientists and biologists), I'm afraid there's just one or two equations which are so often used, they just have to be described. I am going to do this section in morbid detail, because if you have any doubts about these details whatsoever, then electron diffraction, imaging and scattering theory will forever remain a completely closed book for you.
We said above that we need two real numbers to describe a single complex number. In the same way as finding a position on a map, there are two ways of representing the value of the red vector in the diagrams above. We can use two coordinates (like three miles east and four miles north) as in the diagram above, except in the complex plane we have a distance in the 'real' direction and a distance in the 'imaginary' direction. Or we can use one direction and one length, like five miles in a direction of 30 degrees east of due north. With complex numbers, this total distance is the equivalent to the radius of the corkscrew, and is called the 'modulus' of the complex number. The angle is the 'phase' of the complex number. In the complex plane, the phase is alway measured from the real axis, which points due east, and in an anti-clockwise direction, quite unlike the clockwise angles from due north on geographical maps.
Let the real part of a complex number be 'a' and the imaginary part be 'b'. Let the modulus of the complex number be M and its phase be φ. These are then are the two ways of representing one complex number (the red vector):
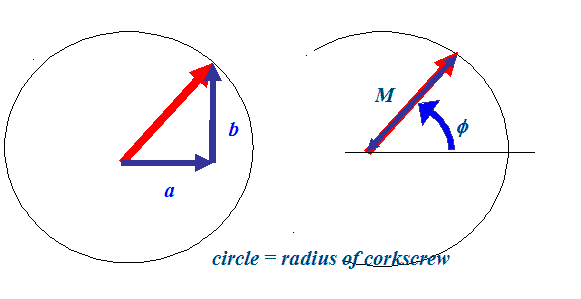
There is a way of relating these two pictures mathematically. The rule is:
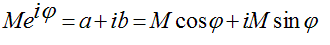
e is just a number (slightly larger than 2.7) and i is defined by the mathematicians as the square root of minus one, and is called the 'imaginary number'. (If you want to prove this relationship, expand e, sine and cosine as a Taylor series, remembering that i squared is minus one.) Lets define a distance along the length of our corkscrew as 'x'. If we put 'x' in the place of φ, then our electron wave value, which I will call ψ, can be written:
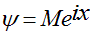
As x increases, the red vector moves around and around the complex plane, describing a spiral, just like the corkscrew.
In practice, we often want to change the 'pitch' of the corkscrew, and we can do this by putting a number that scales how quickly the corkscrew rotates as a function of distance 'x'. This number is designated 'k', so that
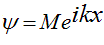
The distance it takes for the corkscrew to rotate one full cycle is called the 'wavelength' of the electron wave. If we think of the shadow of the corkscrew, then for big and small k's we have, respectively, small and big wavelengths, like this:

The phase of the electron wave is not measured in degrees, it is measured in radians, of which there are 2π in 360 degrees, as so we can see that, the wavelength λ = 2π/k: a very fundamental relationship in electron microsocpy. Physically, k is proportional to the momentum of the electron in free space.
Time dependence
Waves move: that is our common experience of the world - waves on the sea never stay still. The same is true for electron waves, but in fact the way they move in time is not very important for most of imagining and diffraction physics. The reason is that all we can ever measure of an electron wave is its intensity, that is to say, the square of the radius of the corkscrew (the modulus squared). Like sea waves, the electron wave is forever changing - but remember, it does not move up and down, its value forever circles around the complex plane.
To demonstrate this, take a real corkscrew and cast its shadow onto a piece of paper. Now rotate the corkscrew, as if opening a bottle of wine. The shadow will seem to move like a wave. Remember, unlike the entire corkscrew, the shadow is not the complete picture of the electron wave. We can describe this mathematically by just adding another phase change (the angle of the corkscrew) to the kx term we introduced above, but one that varies with time, t. Again, we introduce a constant so that we can vary the rate of turning the corkscrew, which we call ω. The total time dependent wave function for a free electron wave is then written out as:
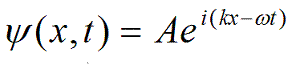
Whenever you see this equation, think 'corkscrew'. The first thing to note is the minus sign in the exponential. If you repeat your turning corkscrew experiment carefully, you'll note that if you turn the corkscrew in the same sense as the pitch of the corkscrew, the shadow moves backwards. To get a forward-travelling wave, you must turn the corkscrew in the opposite sense: that's why we put in the minus sign in the equation above. Of course, backward-travelling waves are equally valid, but conventionally we prefer to discuss waves that move forward in the microscope, from the source down to the phosphor screen.
In the above equation, we have two other minor modifications. The x and the t in brackets after the ψ simply emphasise the fact that ψ depends upon both position and time. We have replaced the modulus M with a general amplitude A, which in practice can itself be a complex number. This is because it is not necessarily the case that when x and t are zero (so that the exponential term is unity), the phase of the wave function is zero. It may have both real and imaginary parts at this point in space, depending on the particular circumstances.
Physically, ω is proportional to the energy of the electron.
One last but important point. When we see the shadow of the electron wave corkscrew moving, we might think this is related to the speed of the electron as it travels through the microscope. This is completely wrong. The speed of the shadow of the corkscrew is called the 'phase velocity' of the electron wave. The speed of the electron itself is governed by a different entity - the 'group velocity' of an electron wave packet. We need to add together lots of different electron waves with slightly different ω's and k's to get such a packet. Because we normally assume all our electrons in the electron microscope have the same energy (same ω, proportional to energy, same k, proportional to momentum) then this time-specific concept of a physically travelling clump of electron cannot occur (it does occur, but not in a way that affects most of our results - it can be important in the details of partially coherent and holographic experiments - but lets not worry about that just yet).
In practice, we can safely forget about time dependence of the wave function. What matters is phase changes between different components (or paths, or 'rays') that arise in the microscope. This gives rise to static (time invariant) patterns of intensity (images, diffraction patterns, etc). The path lengths taken by different beams (corkscrews) is simply a matter of geometry.


Copyright J M Rodenburg
| 
