Electron wave interference:
The single most important property of an electron wave (corkscrew), is that when it encounters another electron wave component (another corkscrew - this 'other component' is still part of the physical description of a single electron), then the complex values of the two wave components add according to the rule of vector addition. Graphically, what this means is as follows. Imagine two corkscrews which, by some means or other, meet up with one another. The total wave disturbance at the point where they meet is given by the addition of the two corkscrew vectors, like this:
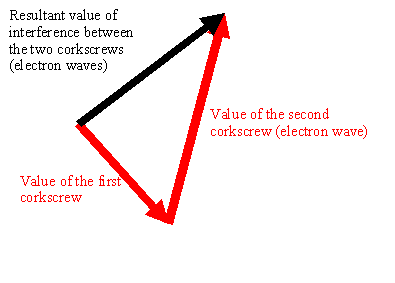
Remember, each corkscrew vector is just a line drawn between the centre of the corkscrew and the edge of the spiral of the corkscrew at one particular point along the length of the corkscrew.
In terms of complex numbers, addition means that we add the real parts of the wavefunctions, and then separately add the imaginary parts of the wavefunction. These two results give the real and imaginary parts of the resultant wavefunction. In numbers, we can express a complex number using two real numbers. This pair of numbers can written like [a,b], where a is the real part of the wavefunction and b is the imaginary part of the wavefunction. The rule of addition for two complex numbers [a,b] and, say, [c,d] is simply:
[a,b] + [c,d] = [a+c, b+d]
This is simply the rule of vector addition.
This idea of the addition of wavefunction may seem trite and rather simple-mind. However, if you fully understand this one concept, then a vast array of wave interference phenonema will be made understandable. All electron imaging and diffraction theory is based on the addition of wavefunctions. This essential and underlying principle of quantum mechanics is called the principle of superposition.
Measurement of Intensity
At some point in the microscope, we make a measurement, usually at the phosphor screen, on photographic film, or on a CCD camera.
It is an axiom of quantum mechanics that when we do this, the probability of detecting an electron is proportional not to the amplitude of the wavefunction (the length of the black vector above), but to its length squared, which is called its intensity. Furthermore, all the phase information is lost. Mathematically, we achieve this by multiplying the wave value by its complex conjugate. The complex conjugate of a complex number [a,b] is simply [a,-b].
The rule for muliplying complex numbers actually defines the main difference between ordinary vectors and the behaviour of complex numbers, and all arises from the definition the imaginary number, i. Basically, when you multiply i by itself you get minus one, so that the product of two complex numbers [a,b] and, say, [c,d] is defined as:
[a,b].[c,d] = [a.c-b.d,a.d+b.c]
where dots mean multiplication, and a,b,c and d are all real numbers. What this means is that a complex number times its conjugate is just
[a,b].[a,-b]=[a.a+b.b,0]
which has zero imaginary component: it is a purely real number. The size of this number is just 'a squared' plus 'b squared,' which we can see by Pythagoras, and the triangle of real and imaginary parts:
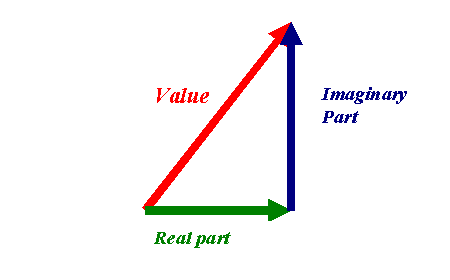
is the length of hypotenuse - that is, the amplitude or modulus (the radius of the corkscrew) - squared.
As the electron wave passes through the microscope and gets scattered by the specimen, we have to keep track of the full complex amplitude of how it changes. It is only when the wave is finally detected that this intensity-forming process occurs. We could at this point have a long discussion about why quantum mechanics works like this: as an electron microscopist, just accept that it does!



Copyright J M Rodenburg
|

