Huygen's Principle

Suppose that instead of having just two gaps, like in Young's slits experiment, we have a substantial gap in our harbour wall. How do we work out the wave amplitude (and, if necessary, the wave intensity) of the disturbance downsteam of the gap? Well, the answer is, we just have to add up lots and lots of 'phase threads'. We make up the gap out of lots of very small elementary gaps. Each elementary gap radiates a spherical wave. At a particular point in space somewhere downstream of the gap, we bring together all the phase threads from each elementary gap, and then add all their respective complex values (which will be pointing in all sorts of different directions in the complex plane, depending on the exact lengths of their corresponding phase threads).

Herein lies nearly all the mathematics of diffraction and imaging theory.

This act of breaking down a wave front (whatever is passing through a particular plane - like the gap in the harbour wall) into lots of little spherical waves is called Huygen's Principle (or the Huygens-Fresnel principle).

Consider the following picture. We want to work out the wave value at a point, P. We have a plane wave incident upon an aperture (harbour wall gap). At every point within the gap, we replace the incoming plane wave with a radiating spherical wave which starts off with the same phase as the incident plane wave. All we have to do is add together the complex values of all the threads that extend from all the elementary points in the gap to the point, P. Here are the threads:

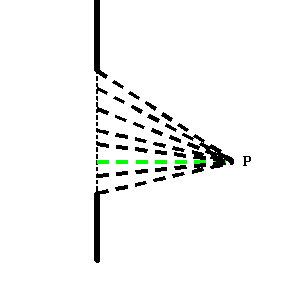
To make the discussion easier, the diagram has one green thread, which, as before, we will define as having zero phase at the point P. The threads either side of this green thread are almost exactly the same length as the green thread, and so their complex amplitudes will add together in just about the same direction as that of the green thread, like this

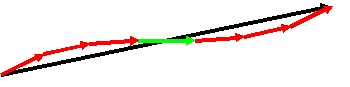
It's pretty obvious that as we consider threads that extend from points further and further away from the green thread, then their phase begins to rotate rapidly. You can try to work out an exact mathematical expression for this using trigonometry (it is very tedius). All I want to express here is a qualitative understanding. If we were to add up all the little vectors in the complex plane, they would do something like this:

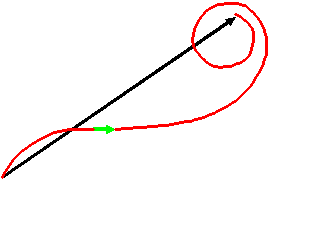
I haven't drawn every individual red vector in this diagram. The red curve just shows how the phase vector of each successive thread (each one further away from the green thread) will add. The curve spirals more and more tightly, because each successive further thread is longer than the previous thread. The lower half of the spiral is shorter than the upper half to reflect the fact that our point P in the first diagram not on the centre-line of the aperture gap.

Less important details:

For completeness, before we discuss the consequences of this strange spiral, there are one or two other details I should mention.

What we have not properly discussed so far is the change in modulus of a spherical wave as it propagates from a source. In order to conserve the total flux of electrons being emitted from a point, the intensity of a spherical wave must decay as a function of 1/(R squared) - just like the intensity decay of a light source - where R is the length of the phase thread. This means its modulus must decay as 1/R. In other words, the complex vectors adding up in the complex plane will be modified in length according to this extra factor.

To make Huygen's principle work, we also can't just substitute a pure spherical wave at each point across a plane, because we will also end up with waves travelling backwards. To stop this happening, we have to put in a further factor into the amplitude of the wavelets, so that as a function of angle, most of their amplitude is in the forward direction. This is called the obliquity factor

If we want to work out quantitative results, we must also scale the amplitude of each spherical wave by 1/(wavelength).

Finally, we might wonder what happens if we take away the harbour wall entirely. Clearly, all that happens now is the plane wave carries on as before. But this means that if we add up millions of spherical waves, all emanating from a flat surface of constant phase (where the harbour wall used to be) then if Huygen's principle is correct, we should just end up with a plane wave! Well, the answer is, we do (provided we include the modifications above). In fact, if you work through the mathematics in detail, it turns out that this new wave has the wrong phase by ninety degrees. In other words, to make Huygen's principle work exactly, the wave disturbance we replace at any point in space must be out-of-phase with the original wave by a factor of i, the imaginary number.

I'm not going to write out all the mathematics in detail here, because all you need to understand most wave phenomena in the electron microscope is just the simple qualitative understanding of the addition of amplitudes governed by phase threads. If you are interested in seeing all of this derived formally, then perhaps the best book is Born and Wolf, 'Principles of Optics' (ISBN 0521 642221).

Copyright J M Rodenburg