Young's slits

With the pair of threads experiment on the previous page, you can spend many happy hours working out the pattern of waves that occupy three-dimensional space lying beyond two small gaps, which are radiating coherently (that is, both gaps are illuminated by a single plane wave).

On this page, we are going to worry about the pattern of intensity caused by same sources over a curved hemi-spherical surface, centred between the two gaps. For simplicity, we'll think of the experiment in two-dimensions, in which case the surface is a semi-cicular line. If we were to extend a third thread from this centre point, then its phase would be constant at all points on the semi-circle, because its total length is always just the radius of the semi-circle. In the next diagram, we draw this thread and the semicircle as green.

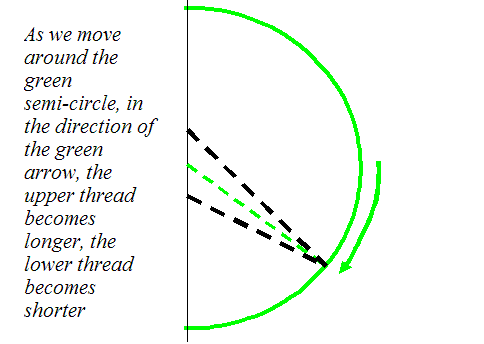
The advantage of all of this is that we now have a reference surface (called a Gaussian surface) over which we can discuss the relative motion (and hence phase) of any other thread which is not attached to (that is, radiating from) the centre of the semicircle. In the case our two threads attached to positions either side of the centre of the semicircle, then clearly, as we move in one direction around the semi-circle, one thread gets continously longer, while the other thread gets continuously shorter. We can measure their respective phases with respect to the green thread, which by definition we will give zero phase (its complex value is pointing in the real direction in the complex plane). As we move around the green circle, then in the complex plane the two (red) wave values add like this.

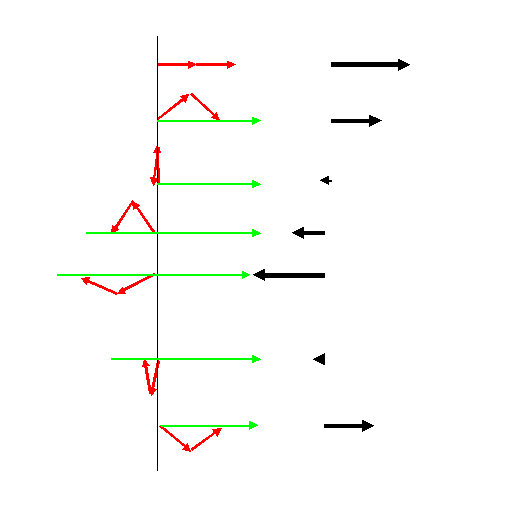
From top to bottom, we are plotting the addition of the complex values (red vectors) arising from the two phase threads as we move around the green circle in the previous diagram. The resultant wave value is a real vector (shown on the right) that varies in length periodically. We could plot the length of this vector as a function of the distance we have moved around the green circle. It would look like this.

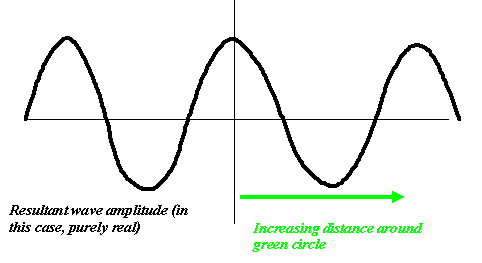
But remember, if we were to put move a detector around the green circle, and measure the intensity of the electron flux arriving at any particular point, what we would measure is the modulus squared of the resultant wave function, and this would look like this:

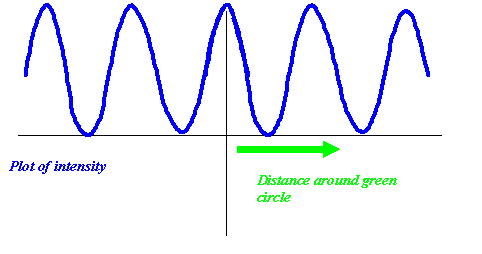
Of course, the intensity of the wave is always positive. The fringes of intensity vary twice as rapidly (as a function of the distance we move around the green circle) as the variation of the underlying wavefunction. [This point impacts in a very important modern field of research called iterative phase retrieval]

What we have described here is a very important historical experiment, first performed by Young using light. The gaps in the 'harbour wall' that he used were slits, but the result is the same around the green circle (now a cylinder in three-dimensional space). It is called Young's slits experiment. It works with electrons, and is a central gedanken ('thought') experiment in quantum mechanics, for reasons to do with wave-particle duality.

What is important for us to understand is that this experiment is the simplest example of wave interference, between just two wave components. In electron microscopy we often deal with thousands or even an infinite number of elementary wave disturbances interfering one another. But this is just an extension of ideas we describe above. If you don't understand Young's slits, you will not understand anything that follows.

Copyright J M Rodenburg