The calculus of wave interference
Water waves and quantum-mechanical waves are governed by an underlying dynamic described by a wave equation. The analogy is not exact, but even if it was exact, it is not obvious how to go about working out exactly how any type of wave is going to slosh about to give us something concrete, like an image or a diffraction pattern. It turns out that we can make some pretty big approximations that give almost the right answer in any situation that is likely to interest us.
All the textbooks introduce these methods using things like Fourier transforms and Fresnel propagators, which very quickly scare off the material scientists and biologists. In this guide, I am going to try to do the same thing using just my notion of phase threads and interference. What follows is an approximation, but it is very nearly exactly what happens in an electron microscope.
Think back to our harbour wall. Imagine the gap in the harbour wall is very, very narrow. If we look from above, the lines of constant phase (or in the case of water waves, the lines of equal height) look like this:
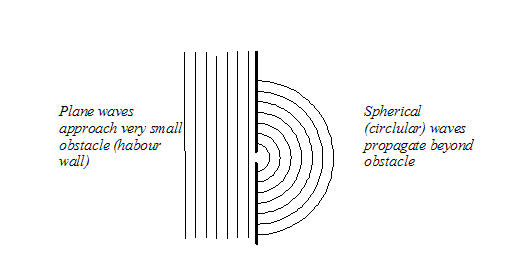
On the left-hand side, we have a plane wave (all phase threads are parallel). On the right-hand side we have what looks like a spherical wave (or, in this two-dimensional analogy, a circular wave). These two types of wave are elementary solutions to the wave equation. The quantum mechanical wave equation is a linear differential equation. That means that if we add together any two (or more) solutions of the wave equation, we get something which is also a solution to the wave equation. In fact we can make up any (even the most complicated) wave disturbance - for example, the whole wave function inside an entire electron microscope, including all the scattering that goes on in the specimen and all the aberrations introduced by the lens - by just adding together elementary solutions of the wave equation. This is what theoretical electron microscopists do.
What we are going to do is add together our phase threads, and we are going to start with the very simplest example.
Supposing we have two tiny gaps in the harbour wall. On the left hand side we still have an incident plane wave. On the right-hand side, we have two spherical waves. The interference (addition) of these two waves, is what we want to work out. Phase threads go off in all directions from each gap, like this:
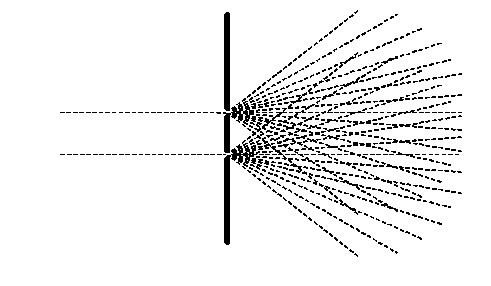
But in order to work out the amplitude of the electron wave at any one particular point in space, all we have to do is worry about the two threads that extend from each gap to that particular point.
Experiment: You can do this at home (if you do it in the laboratory, people will think you are crazy) with real thread. Get two pieces of thread and tie them to two points separated by a few centimetres. Now walk about the room, several metres from where the threads are attached, but keep the threads taught, and brought together tightly between your fingers. This is what the arrangement looks like:
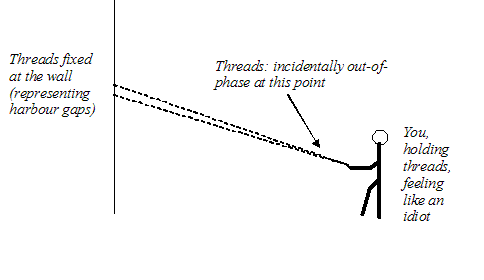
Obviously, as you move away from their points of attachment, both threads move through you fingers. But if you also move sideways, the threads move relative to one another. Remembering our phase threads, they will, at certain places, come to be 'in phase' like this:

Or, sometimes completely out-of-phase, like this:

Or more often, just at some random phase relationship.
Now, to work out the value of the wave at any position, all we have to do is add (by vector addition), the two complex values determined by the phase and modulus of each of the two phase threads. When the two threads are in phase, the vectors add like this:
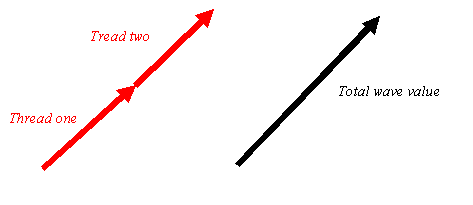
When they are out phase, they add to give nothing, like this:

And when they are some general phase relationship, they add to give something in-between, like this:

In this way, we can work out the amplitude of the electron wave anywhere downstream of the two gaps. It all just depends on geometry of the threads.



Copyright J M Rodenburg
| 
