Reciprocal space, the Ewald sphere and the electron microscope
So far, I’ve described reciprocal space in terms of the Fourier transform and scattering in terms of Bragg reflections from planes of atoms. These are two very different approaches to the same physical phenomenon. In this page, I want to emphasise how they connect to one another, while at the same time describing the Ewald sphere construction.
Let’s start by re-deriving the scattering integral, in other words, the addition of all phase thread corkscrew functions, as in the diagram we used before:
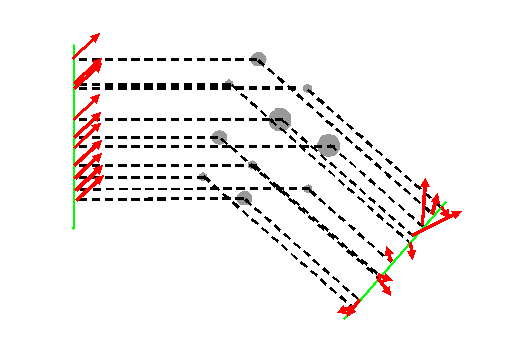
We can write this down mathematically by just thinking about two phase threads, one which is scattered by an atom at the origin of real space, the other which is sitting at some general position defined by the three-dimensional vector r. So, going back to our original phase thread construction:
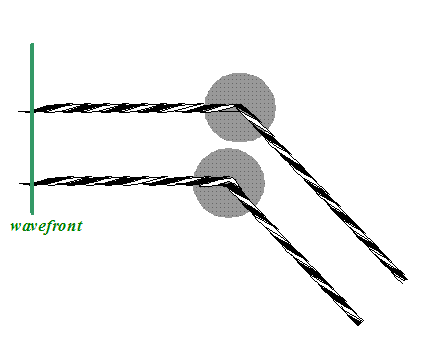
Let’s now think about the relative phase difference introduced into the two phase threads. If we put the lower atom at the origin of real space, then we can redraw the picture more formally as follows:
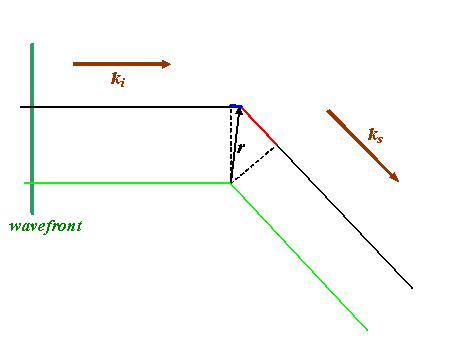
I’m using the same convention I used on previous pages, colouring the thread scattered at the origin (where r is zero) as green: this is our reference thread. We will always assume this phase thread has zero phase. All other phase threads have some phase relative to the green thread.
From the diagram above, the extra phase added to an atom scattering at position r is the path length difference (the addition of the lengths of the blue and red lines) divided by λ and multiplied by 2π. So, we have to work out the lengths of the blue and red lines, using only r and the fact that we know the directions of the incident and scattering vectors (remember, these are always parallel to our phase threads, as we discussed before).
At this point, the textbooks just usually state the answer, but I’m going to go through the calculation in morbid detail, because if you miss this step, you will be lost forever in the crazy world of reciprocal space.
Let’s zoom in to the bit of geometry that matters:
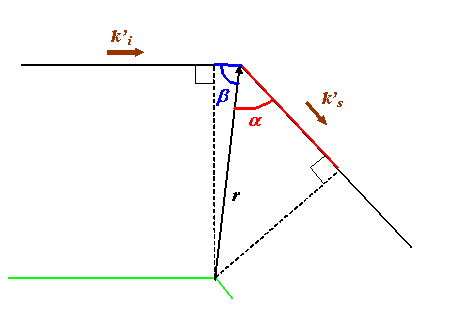
The dashed k-vectors in this diagram are unit vectors, pointing in the directions of ki and ks respectively. From the right-angled triangles, the blue length is r(cosβ) and the red line is r(cosα), where r is the length of r. By definition, the dot product of k’i.r is also r(cos β) (remember the length of k’i is 1). In the case of k’s.r we have to be a little bit more careful. Let’s redraw all the pertinent vectors in one diagram, shifting them about so each pair of vectors point from a common origin, as follows:
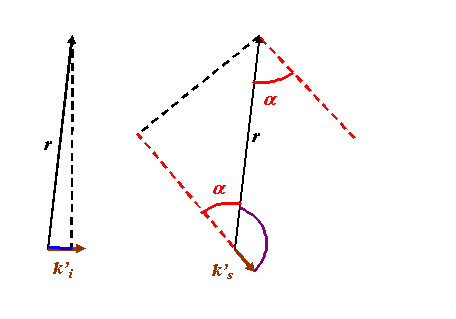
It becomes clear that the purple angle between ks is larger than 90 degrees (it is π - α) and so in this case it would wrong to say that ks.r is the distance we are looking for: it is, in fact, -ks.r (remember that cos (π - α) = - cos α).
All this means that we can write the total path length difference for the atom positioned at r as p, where:
p = k’i.r-k’s.r
Now remember that earlier on we defined K as the scattering vector, which is the k-vector we had to add to ki to get ks: that is, the amount the actual k-vector of the radiation (phase thread) changes as a result of the scattering. We say that
ki + K = ks
or
K = ks-ki.
Now we see from above that the path difference is given by
p = - K’.r
Where K’ is a unit vector pointing in the direction of the scattering vector, K. The total phase change induced by the path difference p is 2πp/λ. But to get ks, ki or K from k’s, k’i or K’, we know we have to multiply the unit vectors by the magnitude of k, namely 2π/λ. That means the total phase difference of the wave scattered by an atom at position r is simply
Δφ = -K.r.
- a surprisingly simple result.
All the shenanigans we went through above, worrying about negative dot products, arises from the particular way the diagram was drawn. In fact, this same result holds true for all orientations/positions of r relative to the real space origin. A particular arrangement which is often drawn in the textbooks looks like this:
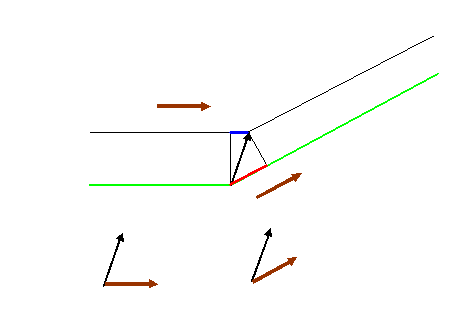
Now, both dot products involve angles which are less than 90 degrees, so they are both positive. However, the path length difference is now the blue line minus the red line (the upper thread is shorter than the green one that goes through the origin), so that means the total phase difference is
Δφ = ki.r – ks.r = -K.r
the same result as before. No matter where r or the incident and scattered k-vectors point, the result is the same.
So that’s easy. It means that if we want to construct the total scattering amplitude in any direction, defined by an incoming beam ki and a scattered beam ks, then we just add up all such phase threads. Remember, the complex value of each thread is e-iK.r. Let f(r) be the strength of scattering at position r. Then the total scattered amplitude, integrated over all scattering points in real space (all r), which we’ll call S(K), is just
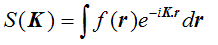
which we should by now recognise as the three-dimensional Fourier transform of f(r).
How does reciprocal space relate to reality?
The astute amongst you will notice there is a minus sign in the exponential of the Fourier transform. I’ll explain this super-minor anomaly below. In the meantime, let’s just understand what we have derived.
The scattering strength at a particular combination of ks and ki is given by the Fourier transform of the scattering object. This Fourier transform is taken with respect to K, which is the vector difference between ks and ki. Remember that ks and ki both have the same magnitude. Because we can think of a Fourier transform as the integral of a product of a corkscrew function and the object, then this Fourier transform has a large amplitude whenever K is perpendicular to a series of planes of the object which are separated by the ‘wavelength’ of this K-vector. This ‘wavelength’ is not the wavelength of the radiation involved in the scattering, it is equal to 2π/K: in other words, it is the separation of the planes of atoms which are doing the scattering. We can come back to the picture we drew before:
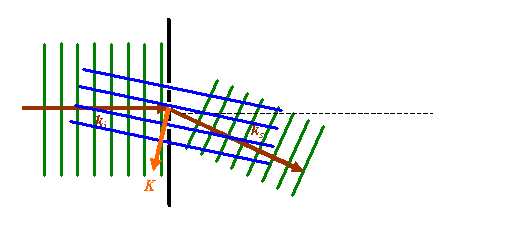
This summarises all the relationships we have discussed. K is perpendicular to the blue scattering planes, which have a separation inversely proportional to the length of K. From this, we derived Bragg’s Law in real space.
However, electron microscopists often find it easier to think in reciprocal space: the space defined by the brown and orange vectors, arranged as follows:
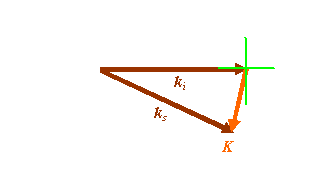
The green cross marks the origin of reciprocal space (the origin of the vector K). To maintain the correct relationship between ks, ki and K, the end of ki must always be fixed to the green cross.
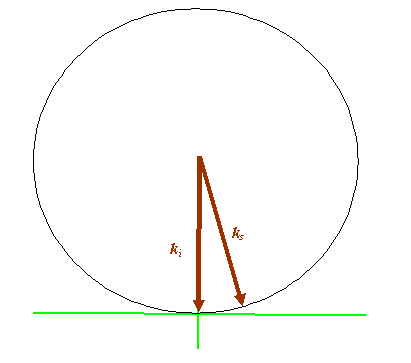
We can use these vectors to think of all the possible ways we can orientate the object, the incident vector and the scattered vector. If we keep both the orientation of the object and the incident direction of the radiation fixed, then possible values of the scattered vector sweeps out a circle – actually a sphere in 3D scattering, like this:
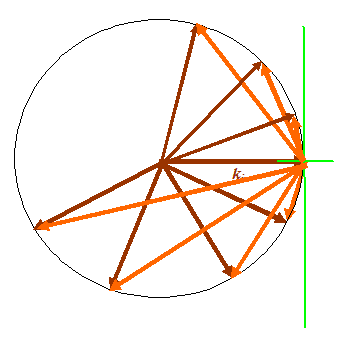
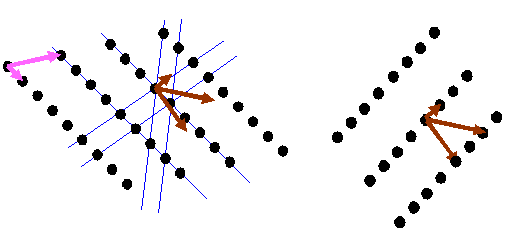
For a crystalline specimen, strong scattering occurs whenever the orange vector coincides with a reciprocal lattice point. So, if we thought of our previous example, then:
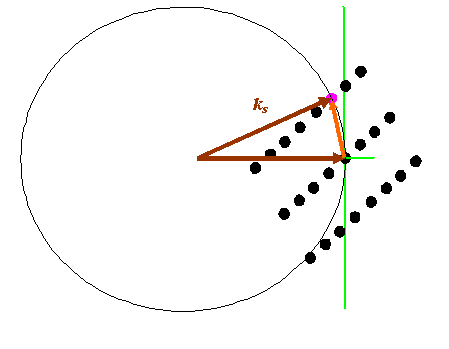
What this means is that for this particular crystal, whose reciprocal space is the series of points shown, then the only direction in which strong scattering will occur is related to the pink dot – that will give rise to strong scattering in the ks direction – but remember, only for this particular incident vector. Back in real space, this is the arrangement of actual atoms:
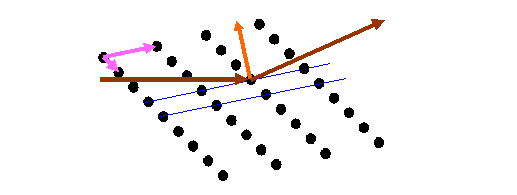 where the blue lines the planes of atoms we would use in the Bragg construction. Remember, the relationship of the dots in the two diagrams above is that one is the Fourier transform of the other, as we discussed earlier. The two lattices (real and reciprocal) are related as follows:
where the blue lines the planes of atoms we would use in the Bragg construction. Remember, the relationship of the dots in the two diagrams above is that one is the Fourier transform of the other, as we discussed earlier. The two lattices (real and reciprocal) are related as follows:
Electron microscopists draw the sphere of possible K-vector that satisfy a scattering condition (as shown above) - called the Ewald sphere - in the orientation natural to an electron microscope: that is, with the incident vector pointing down vertically. After all, the electrons shoot down the column from the top downwards, and so the diagram looks like this:
Once again, back in real space, we can think what is happening in a real electron microscope:
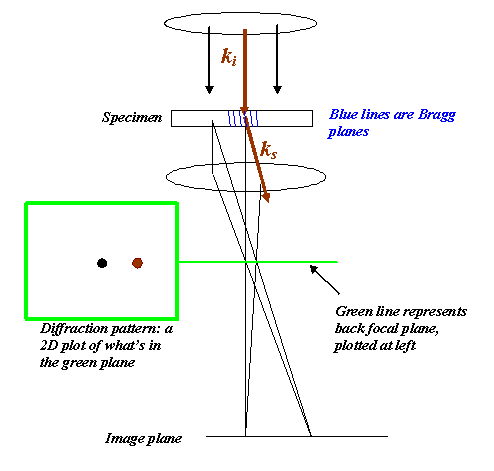
If you are unfamiliar with what this diagram means, then read the elementary TEM guide.
What happens is that the electrons come vertically down the column (the incident beam), through the condenser lens. The electron beams (waves) strike the specimen, which in this diagram has Bragg planes within it which are slightly tilted (this is formally called a ‘two beam’ condition; the two beams being the incident beam and a scattered which perfectly satisfies a Bragg reflection).
These beams propagate from all parts of the specimen to the image plane. On their way, beams which are parallel to one another as they come out of the specimen meet up in the other special plane of an electron microscope: the back focal plane. If we arrange to image the back focal plane on the phosphor screen (by altering the projector lenses), then what we see in a Fraunhofer diffraction pattern. This is a two-dimensional pattern, as shown in the green square. Our ‘straight through’ (incident) beam is drawn as a black dot. The scattered beam is drawn as a brown dot.
Herein lies all the main ideas of electron diffraction as it relates to reciprocal space, the electron lenses and the image plane.
Aside: Why does our Fourier transform end up with a minus sign in the equation above? Well, if we define our corkscrew function with a positive kx in the exponential, then the minus sign has to be there, because of the way an increase in path length increases the phase of the scattered wave. Only atoms below the origin (in a negative r direction) have positive extra path length.
We could have defined our corkscrew function with a –kx (and a positive ωt) in the exponent: this is still a forward travelling wave. In that case, there is no minus sign in the Fourier transform. Remember, our definition of the Fourier transform is purely conventional anyway: the mathematicians and physicists often define the forward transform with a negative exponential.
Suffice to it to say, in these pages, I have tried to minimise the number of minus signs hanging around the place (in the definitions of my waves and Fourier transforms), and so this is where we come unstuck as far as pedantic arithmetic is concerned.
Generally, the crystallographers have ‘negative’ (e-ikx) waves and ‘positive’ Fourier transforms. Historically, many (but not all) electron microscopists do it all the other way round.
I was a bit cunning in earlier pages by defining my positively increasing θ in an opposite sense to my definition of positive x (r), thus avoiding all the minus signs.
Don’t lose any sleep about this…!



Copyright J M Rodenburg
| 
