The scattering vector and plane waves in 3D
So far, we have only discussed one-dimensional waves , travelling along lines (beams or rays), represented by our phase threads. When these waves scatter from a three-dimensional object, such as a group of atoms (whether crystalline or not), then we must really think about what is happening to the waves in three-dimensional space.
Let’s start by understanding fully a three-dimensional plane wave. Our corkscrew function in 3D is defined by the equation
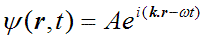
There are only two differences between this and its one-dimensional equivalent. First, instead of being a function of the one-dimensional variable x, it is function of three-dimensional vector r (denoted by bold text). Secondly, k (the pitch or rate of rotation in space of the corkscrew) is now also a vector quantity. Instead of forming a product in the exponential, k and r form a vector dot product.
How does this work?
Well, qualitatively, think of k as a vector pointing in the direction of travel of the wave. That means it’s parallel with the phase threads and perpendicular to the surfaces of constant phase. Remember, a plane wave consists of sheets of constant phase, as in the diagram we discussed before:
The other important thing to remember is that the length of k is inversely proportional to the wavelength of the plane wave: if the sheets of constant phase are close together, k is large; remember that the magnitude (length) of k is defined as 2π/λ: when λ is large, k is small.
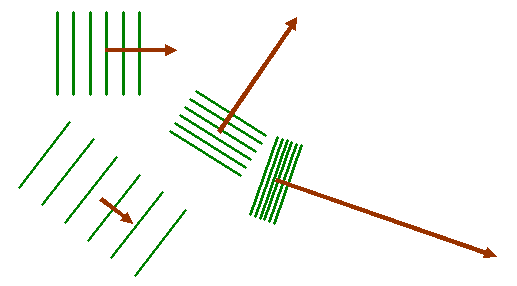
Here are some examples in two dimensions. The surfaces of constant phase are lines coloured green (like lines of constant height in a water wave). The corresponding k vectors are coloured brown.
How does the dot product k.r contrive to achieve this relationship? Well, thinking again in two dimensions, let’s first express the dot product in terms of its component parts:
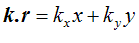
where all the quantities on the right hand side of the equation are just numbers. kx and ky are the x- and y-direction components of the vector k, and the vector r has Cartesian coordinates x and y. Now clearly, if ky is zero, we just have a wave travelling in the purely x-direction, like this:
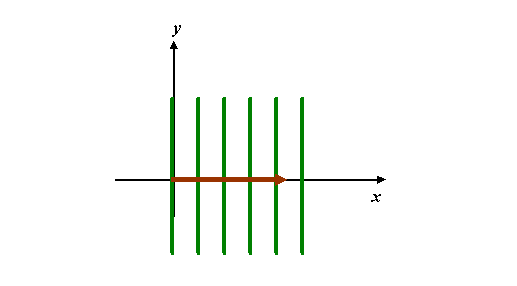
Note that we not plotting y as a function of x in this diagram. x and y are real space coordinates in a two-dimensional plane. Each point in this plane has a complex value associated with it. The green lines map out the points in this space where the phase of the complex value of the wave is zero (or some constant). If we were worrying about time dependence, then the green lines would move towards the right, like waves on water. As before, the k-vector for this wave is drawn in brown: it points in the x-direction (but its length does not have the dimensions of x – being a reciprocal quantity, it has dimensions of 1/x).
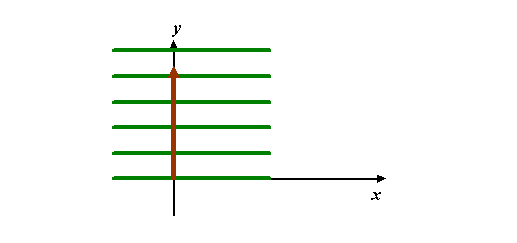
Similarly, if ky is zero, but the magnitude of the k-vector is the same as in the example above, then the plot would look like this:
Now let’s think of a wave with a k-vector consisting of these two k-vectors added together. We add the two x- and y-components according to the rule of vector addition, like this
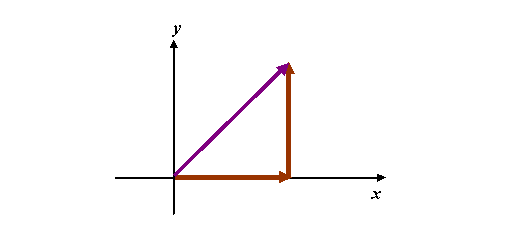
giving the purple resultant k-vector. The wave associated with this k-vector has a higher spatial frequency than either of the brown k-vectors. In fact, using Pythagoras, it is longer by a factor of the Ö
2, implying that the wavelength of the waves associated with this k-vector is shorter by a factor of 1/Ö2. The wave fronts must be perpendicular to it, like this:
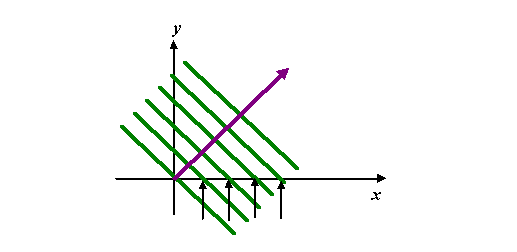
Note that the green lines intersect with the x-axis at equally-spaced intervals, marked by the pointers. The pointers have the same spacing as the green lines of constant phase in the first wave picture, which had a horizontal k-vector. This is because along this line y=0, the exponential term in the corkscrew wave function reduces to
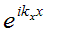
where, as usual, we have ignored the time-dependent term ωt and have assumed the amplitude is unity. Similarly, along y-axis (x=0), we have:
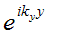
The two-dimensional time-independent wave is
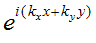
Everything in brackets in the exponential is just a number – the phase of the corkscrew. Lines of constant phase occur when kx+ky=c, where c is constant. Because in this example the lengths of kx and ky are equal, then lines of constant phase satisfy x=-y+c: the parallel green lines in the diagram above. The separation of the green lines can be worked out putting c=2πN, where N is integer. Simple geometry will show that the green lines are spaced by 1/Ö2. Be careful to realise that we are not adding together two waves here (if we did that, we would produce an interference pattern); we are adding the k-vectors of two waves. The resultant wave has a periodicity corresponding to the length of the resultant k-vector. Any combination of kx and ky behaves in the same way.
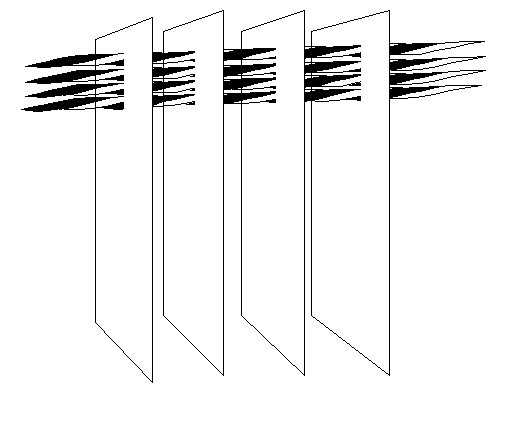
In three-dimensions, think of planes of constant phase. You could make a model of these by using a number of sheets of cardboard. Arrange the sheets of cardboard by piercing them onto a pencil, like this:
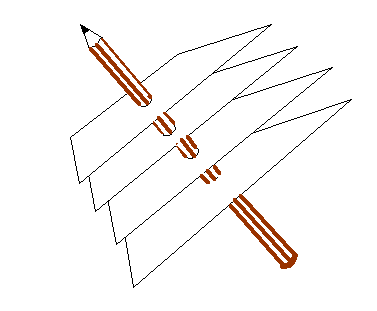
The pencil represents the direction of the k-vector. Its length is inversely proportional to the spacing between the sheets of cardboard. The pencil can point in any direction in space, defined by its Cartesian components: kx, ky and kz.
The scattering vector K
In all our discussions so far, we have not worried very much about the k-vectors of the waves we have been considering. Everything that we wanted to discuss could be thought about in terms of the interference of phase threads. Let’s label the k-vector of the wave which illuminates our object as ki(the ‘incident’ wave). The wave which scattered into some direction in the far-field we’ll label ks (the ‘scattered wave’). When we were thinking of scattered waves in Young’s slits experiment or the diffraction grating, the geometry of the k-vectors would look like this:
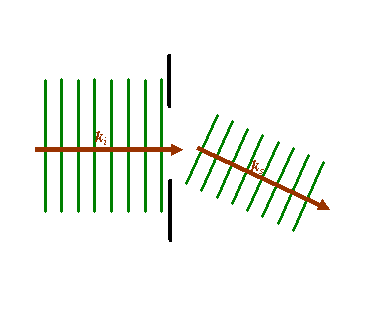
Once again, the green lines are where the waves have constant phase, the brown vectors are the k-vectors associated with these waves (always parallel to the phase threads). We assume that in the scattering process (whatever it is that causes scattering – atoms, slits in a grating, the harbour wall) there is no loss of energy (in general this is not always true, but it easier to start by considering loss-less processes, that is to say ‘elastic scattering’). That means that the energy of the scattered electron is the same as its energy when it was incident upon the object. This, in turn, implies it has the same wavelength throughout the scattering event, and so the magnitude (lengths) of the vectors ki and ks are identical.
What is the change in the incident k-vector which gives rise to the scattered vector? Call this change, K, the scattering vector. Then ki, plus this vector K, gives rise to ks. We can rearrange the vectors as follows:
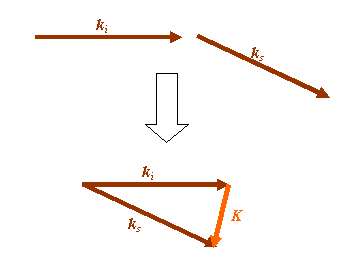
K is what we have to add to ki to end up with ks.
When we discussed the Fourier transform of a diffraction grating, we came to conclusion that the scattered pattern of radiation was given by
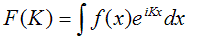
(give or take a minus sign which we'll discuss later) where K was proportional to the scattering angle θ, scaled by the wavelength. We implicitly had assumed that K lay in the same plane as the diffraction grating: in other words, K was vertical in the following diagram:
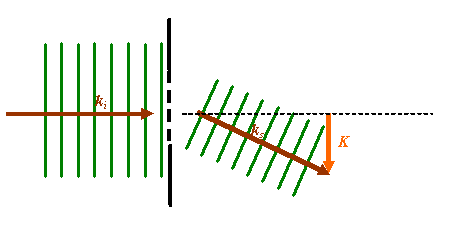
Clearly, the above two definitions of K are not compatible. In fact, for small angles of scatter, which is after all what we assumed in order for the far-field diffraction pattern to be given by the Fourier transform of the wave coming out of the diffraction grating, then the two definitions are identical. At larger scattering angles, and for three-dimensional scattering objects, this simplified relationship breaks down. We must use the proper vector relationship between ki, ks and K. If we had scattering through 90 degrees, the scattering vectors would look like this:
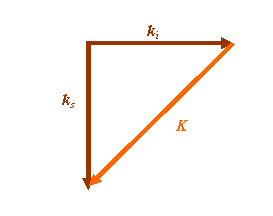
K is now bigger in magnitude than both ki or ks. What does K represent? It actually represents the K-vector of a particular Fourier component in the Fourier transform of the object that is doing the scattering. But before we explain this fully, let’s first think about what’s going on in real space…



Copyright J M Rodenburg
| 
