The Fraunhofer and Fresnel approximations
Our calculus of phase threads is a pretty general principle, but in practice, we often make certain approximations, which are referred to by different names.
Whenever all the phase threads are effectively parallel to one another, then we refer to the resulting diffraction pattern as a Fraunhofer, or Fourier domain, or far-field diffraction pattern. We've already discussed one type of Fraunhofer pattern with our Young's slits experiment. The diagram looked like this:
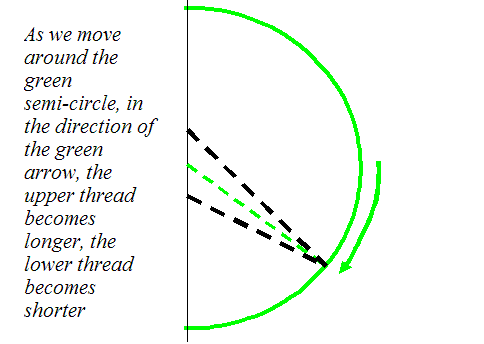
Well, the threads are not perfectly parallel here. But if we were to make the hemi-sphere very, very large, then all the threads would be parallel. The pattern we see would exist purely as a function of angle around the hemi-sphere. The co-ordinates of Frauhofer diffraction are therefore angles (or, more precisely, direction cosines). For all threads to be parallel, the object of interest (in the case above, the separation of the slits) must be small and the radius of the hemi-sphere must be large. How small and how large these dimensions are allowed to be depends on the wavelength, which determines the allowable error caused by the threads not being quite parallel.
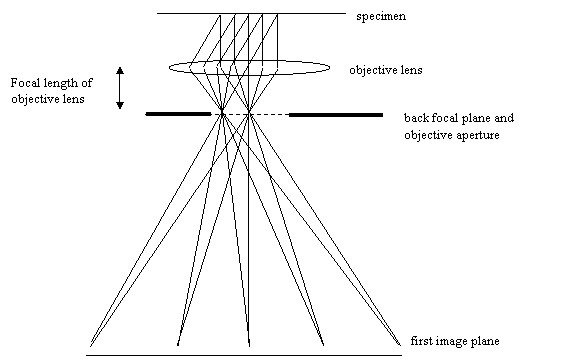
We have an easy way of making a Fraunhofer diffraction pattern in the electron microscope. We just press the 'diffraction' button. Remember, we are imaging the back-focal plane, which by definition is where all parallel beams emerging from the specimen come to a focus:
On the contrary, Fresnel diffraction is the term used whenever we cannot make this 'parallel thread' approximation, in other words when we want to calculate a wave near a source of scattering.
Validity limits of the Fraunhofer approximation:
We can work out a rough expression for when the Fraunhofer condition applies by
considering when the ‘parallel thread’ approximation breaks down. Two parallel
threads subtending from opposite edges of the scattering object, of width D, at some
angle, say θ, have a path length difference between them of p, as shown in the
following diagram:
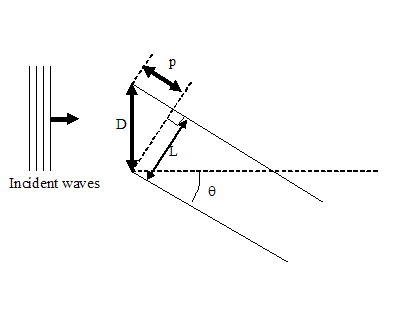
In this diagram, L = D cosθ (we will use this quantity below).
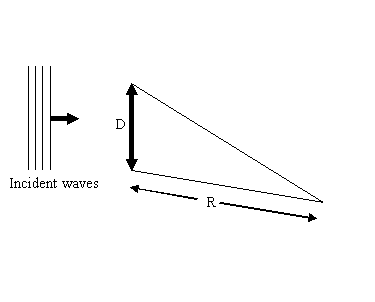
Now in the Fresnel condition, the threads meet up at a position relatively close to the
scattering object, say at a distance R, like this:
If we suppose that the upper of the thread is at the same angle in the two diagrams,
then what is the effect of the path length change of the lower thread being at a
different angle in the two diagrams? Well, imagine holding onto the two threads,
keeping the one upper stationary, we swing the lower thread upwards, like this:
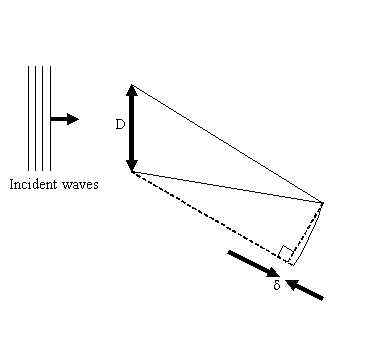
We see that the lower thread describes an arc of a circle, and the extra path length
added to it as a result of no longer being parallel with the upper thread is δ. If we
remember our elementary geometry, then for any two chords of a circle PQ and ST
crossing each other at O, like this
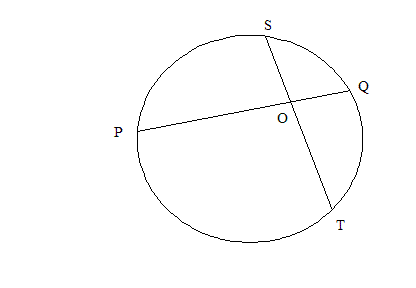
then the lengths PO times OQ equals SO times OT. In our case, we can redraw our
two threads inscribed in a circle of radius R, like this:
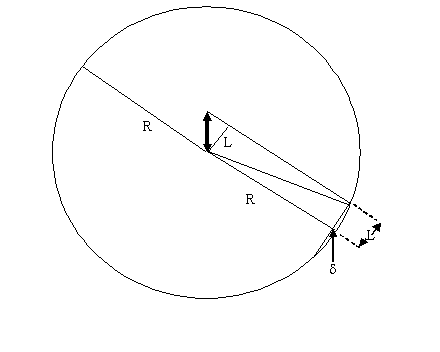
where L is as defined earlier. We see that (assuming 2R - δ is roughly 2R)
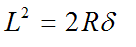
where
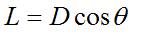 . .
We generally wish to know how large R has to be in order for the Fraunhofer
condition to apply. Clearly, this all depends upon how much of a phase error (caused
by the non-parallel threads) we are prepared to tolerate. The phase error in radians is
given by 2πδ/λ, where λ is the wavelength of our radiation. The total
sum of adding up all the various complex values of our phase threads will be radically
different if the contributions from the extreme edges of the scattering object are
completely out of phase, that is if δ
=λ/2. In practice, we probably want the
error to be much less than λ/2, say fλ, where f is a small fraction. In this case,
the Fraunhofer condition is satisfied if
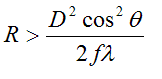 . .
In electron microscopy, the scattering angles are generally small (one to ten degrees),
and so we can further approximate that L is about equal to D. So very roughly speaking, we
reach the Fraunhofer condition when
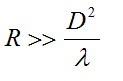 . .
Other important differences between Fraunhofer and
Fresnel diffraction:
1) Movement:
We can formulate the definition of Fraunhofer diffraction from a completely different
perspective: a Fraunhofer diffraction pattern does not move as the object (together
with the illuminating radiation) is moved laterally.
Unless we use a lens to form the diffraction pattern, then if R (the distance to the
recording plane) is very large, the diffraction pattern will not appear to move relative
to the total size of the pattern itself. So for example, if we have an object which is
100nm in size, the electron wavelength is 0.0025nm, and the phase error we are
prepared to tolerate in our phase threads is f =1/10 (a phase error of 36 degrees), then
R must be larger than 200 microns. In any experimental set up, R would typically be
of the order centimetres, and so the Fraunhofer condition is very well satisfied for this
object size.
A typical electron diffraction pattern would extend up to about +/-10 degrees, and so
when R = 200 microns, the total width of the pattern is about 40 microns. Now if we
were to move the object laterally by its width (100nm), the diffraction pattern will
also move by 100nm, but this is only 0.25% of its total width, and so we will not
notice any substantial change in its position. When we use a lens to form the
Fraunhofer pattern, even this tiny movement is eliminated (unless of course we
moved the object so far that the diffracted beams miss the lens entirely! – in fact, for
an aberrated electron lens, there will be a slight movement – but this is not important
in the present context).
In summary, Fraunhofer patterns are fixed in position: they do not move as a function
of shift of the scattering object. On the contrary, a Fresnel diffraction pattern (like
the Fresnel fringes we discussed earlier) is
recorded much closer to the scattering object: these patterns move in a way that
directly corresponds with any shift in the object.
2) Propagation
The term ‘propagation’ in the context of waves means the
act of allowing the wave to move forwards in space and
time. Many wave patterns are stationary, in the sense
that the pattern of intensity of the wave stays the same,
even though the underlying wave continues to move
constantly. Propagation is a mathematical way of finding
out how the shape of the wave changes as it spreads from
one region of space (usually in a plane, like the image
plane or the diffraction pattern plane) to another. In
electron microscopy we usually forget about time
dependence, so propagation is just about finding out how
the wave amplitude changes in space.
Another key difference between Fresnel and Fraunhofer
diffraction is that Fresnel diffraction patterns change
as we propagate them further ‘downstream’ of the source
of scattering, whereas the shape of the intensity of a
Fraunhofer diffraction pattern stays constant. In fact,
as far as any real physical detector is concerned, as we
move further and further away from the object, the
Fraunhofer pattern gets bigger and bigger, and its
intensity at any one point gets smaller (although the
overall integrated intensity remains constant): however,
its overall shape does not change. This is because the
Fraunhofer pattern is a function of angle only. Once R
is large enough to satisfy the Fraunhofer condition, the
relative phase of the threads at any one angle do not
change as R increases further.
On the contrary, a Fresnel diffraction pattern
does change in shape as we move further away from
the object (until, of course, we are so far away that the
Fraunhofer condition is satisfied). It is easy to
understand this in terms of phase threads. When we are
close to an object of substantial size, the phase threads
are extending towards us over a range of angles, like in
the diagram we used earlier:
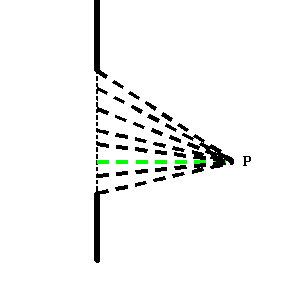
It is pretty clear that as we move the point P away from
the object (hence we propagate the wave towards the
right) then the relative lengths of the phase
threads change with respect to one another. If the
wavelength is short, even small changes in the relative
length of the phase threads will radically affect the
final result we obtain when we add up all the complex
values corresponding to each thread.
In summary, near a source of scattering, the shape of
wave changes substantially as we move away from the
object. Eventually its shape settles into a Fraunhofer
diffraction pattern (when R is large, given the size of
the object and λ). From that point onwards, the
shape of the wave intensity just physically expands as we
move away even further, but its shape stays the same.
(Aside: If we form a Fraunhofer diffraction pattern
using the back focal plane of a lens, then it is not true
that if we move away from this plane – i.e. propagate the
wave – that the pattern we observe remains the same.
This is because of the way we are using the lens to bring
what were parallel beams (threads) to a focus where they
interfere. This focus occurs only at one very distinct
plane, because the beams incident upon it are not
parallel to one another, but are converging over a range
of angles.)
3) The surface of calculation:
In the examples we’ve shown here, we have chosen to
calculate Fresnel diffraction patterns on flat surfaces
and Fraunhofer diffraction patterns on spherical
surfaces. I think this is the logical way of approaching
the subject, although it is not the way most textbooks
derive the mathematics. The usual diagram is shown as
follows:
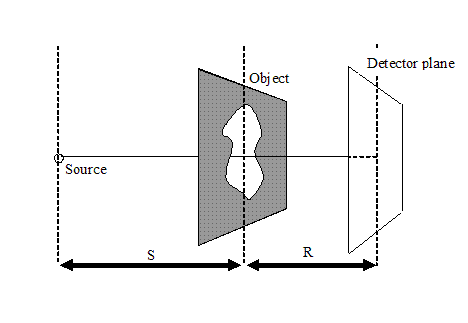
A source is position a distance S away from a flat
surface, where some sort of aperture or object is
positioned. A detector plane, also a flat surface, is
positioned a distance R away on the other side of the
aperture or object plane.
In our discussion above, we always assumed that the
object was illuminated by a plane wave, which is
equivalent to saying that S, the distance from the source
to the object, is very large (in fact, the definition of
‘very large’ is the same as for R being large for the
Fraunhofer condition to apply). As we move our detector
plane from R=0 to R = large distance, then the pattern we
record will start off as simply the intensity of the wave
at the exit surface of the object function, it will then
develop into a Fresnel pattern (complete with all the
Fresnel fringes we discussed earlier, if there are sharp
edges in the object), and then, as R is large enough to
satisfy the Faunhofer condition, it will turn into a
Fraunhofer pattern, from then on just getting larger and
larger.
The trouble with this formulation is when we want to
think about the phase of the underlying Fraunhofer
diffraction pattern. Over a flat surface, the phase of
the wave changes rapidly as we move away from the centre
of the pattern, irrespective of whether we are in the
Fraunhofer condition or not, as shown in the following
diagram:
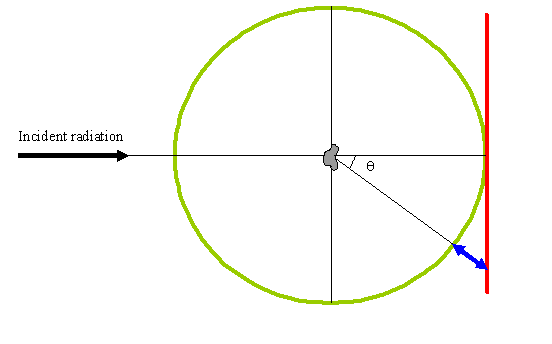
Here, the red line is a section through a flat detector
plane, as in the conventional formulation. The green
line is a section through a spherical surface, centred on
the centre of the object function. We used the right of
half green line in our discussion of Young’s slits.
The problem with the red line is that the underlying
phase of the diffraction pattern over its length changes
very rapidly as a function of θ, because of the
extra path difference shown in blue. In fact, in the
Fraunhofer condition, this extra path length difference
(and hence phase change) has no bearing on the recorded
intensity (except for a decay factor due to 1/R2), because all the contributing phase threads
have the same path length (phase) added to them. The
complex value of the wavefunction may vary very rapidly
along the blue line, but its modulus (and hence
intensity) remains constant.
Now, it is often said that the Fraunhofer diffraction
pattern is the Fourier Transform of the exit wave coming
out of the object function. In fact, the complex value
of the wave over a flat surface (i.e. along the red line)
is not the Fourier Transform of object exit wave.
However, over the green line (a hemispherical surface)
the complex value of the wave is mathematically
equivalent to the Fourier Transform, at least for small
values of θ.
In my experience, this little detail leads to all sorts
of confusion.
First, it is sometimes said that validity of the
Fraunhofer condition for the phase of the scattered wave
is much more severe than for its intensity. That’s true
if we insist upon talking about flat detectors (or flat
planes on the entrance pupil of lenses that re-interfere
the diffraction pattern) because of this extra path
length. But in general it is much more natural to define
the Fraunhofer pattern over a sphere, in which case this
issue just doesn’t arise.
Secondly, because most the textbooks start off with a
flat detector surface (which is, after all, not
unreasonable), this extra ‘flat surface’ phase change is
incorporated into the diffraction integral. Only by
forming the intensity (which is often asserted quite
early in the conventional derivation) is this extra phase
obliterated (the wave is multiplied by its complex
conjugate). However, this means that the direct
connection between the mathematical device of the Fourier
Transform and Fraunhofer diffraction plane is lost. Most
texts undertake a change of coordinates (from the flat
surface to angles of scatter) in order to bring out the
equivalence. If we stick to the spherical surface (the
green line) from the start, we don’t suffer any of these
messy complications.
Another good reason for using the spherical surface is
that (given appropriate scaling) it is equivalent to the
Ewald sphere, an indispensable tool in all diffraction
theory (that is, Fraunhofer diffraction theory) of the
scattering of waves from three-dimensional objects. The
green curve is then seen truly as a subset of a three-
dimensional Fourier Transform of the object function,
even at large values of θ (which in the diffraction
literature is called 2θB, where θB is called the Bragg
angle). This is even true for waves which have been
scattered through an angle greater than 90 degrees.



Copyright J M Rodenburg
| 
